Reducing a Stream

Calling a Terminal Operation on a Stream

So far you read in this tutorial that reducing a stream consists of aggregating the elements of that stream in a way that looks like what is done in the SQL language. In the examples you ran, you also collected the elements of the streams you built in a list, using the collect(Collectors.toList()) pattern. All these operations are called terminal operations in the Stream API and consists in reducing your stream.

There are two things you need to remember when calling a terminal operation on a stream.

1. A stream without a terminal operation does not process any data. If you spot such a stream in your application, it is most probably a bug.
2. A given stream instance can only have one intermediate or terminal operation call. You cannot reuse a stream; if you try to do that, you will get an IllegalStateException.

Using a Binary Operator to Reduce a Stream

There are three overloads of the reduce() method defined in the Stream interface. They all take a BinaryOperator object as an argument. Let us examine how this binary operator is used.

Let us take a example. Suppose you have a list of integers, and you need to compute the sum of these integers. You can write the following code to compute this sum, using a classic for loop pattern.

List<Integer> ints = List.of(3, 6, 2, 1);

int sum = ints.get(0);
for (int index = 1; index < ints.size(); index++) {
    sum += ints.get(index);
}
System.out.println("sum = " + sum);

Running it prints out the following result.

sum = 12

What this code does is the following.

1. Take the first two elements of the list and sum them together.
2. Then take the next element and sum it to the partial sum you have computed.
3. Repeat the process until you have reached the end of the list.

The way this computation is conducted can be summarized on the following figure.

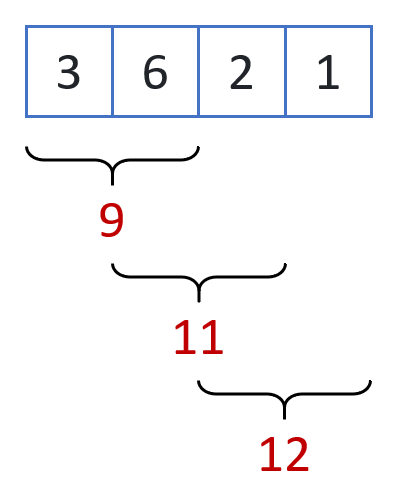
If you check this code carefully, you can see that you can model the SUM operator with a binary operator to achieve the same result. The code then becomes the following.

List<Integer> ints = List.of(3, 6, 2, 1);
BinaryOperator<Integer> sum = (a, b) -> a + b;

int result = ints.get(0);
for (int index = 1; index < ints.size(); index++) {
    result = sum.apply(result, ints.get(index));
}
System.out.println("sum = " + result);

Now you can see that this code only depends on the binary operator itself. Suppose you need to compute a MAX. All you need to do is to provide the right binary operator for that.

List<Integer> ints = List.of(3, 6, 2, 1);
BinaryOperator<Integer> max = (a, b) -> a > b ? a: b;

int result = ints.get(0);
for (int index = 1; index < ints.size(); index++) {
    result = max.apply(result, ints.get(index));
}
System.out.println("max = " + result);

The conclusion of this is that you can indeed compute a reduction by just providing a binary operator that operates on only two elements. This is how the reduce() method works in the Stream API.

Choosing a Binary Operator That Can Be Used in Parallel

There are two caveats you need to understand though. Let us the first one here and the second one in the next section.

The first one is that a stream can be computed in parallel. This point will be covered in more detail later in this tutorial, but we need to talk about it now because it has an impact on this binary operator.

Here is how parallelism is implemented in the Stream API. Your source of data is split in two parts, each part processed separately. Each process is the same process as the one you just saw, which uses your binary operator. Then, when each part is processed, the two partial results are merged with that same binary operator.

Here is how this computation is conducted.

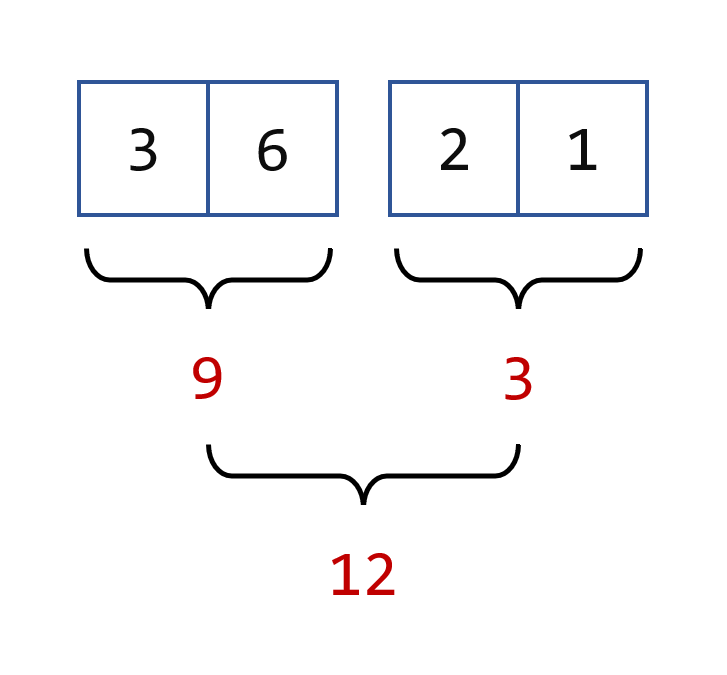
Processing a stream of data is very easy: it is only a matter of calling parallel() on a given stream.

Let us examine how things are working under the hood, and for that, you can write the following code. You are only simulating how to conduct a computation in parallel. This is of course an overly simplified version of a parallel stream, just to explain how things work.

Let us create a reduce() method that takes a binary operator and uses it to reduce a list of integers. The code is the following.

int reduce(List<Integer> ints, BinaryOperator<Integer> sum) {
    int result = ints.get(0);
    for (int index = 1; index < ints.size(); index++) {
        result = sum.apply(result, ints.get(index));
    }
    return result;
}

Here is the main code that uses this method.

List<Integer> ints = List.of(3, 6, 2, 1);
BinaryOperator<Integer> sum = (a, b) -> a + b;

int result1 = reduce(ints.subList(0, 2), sum);
int result2 = reduce(ints.subList(2, 4), sum);

int result = sum.apply(result1, result2);
System.out.println("sum = " + result);

To make things explicit, we have split your source of data in two parts, and reduced them separately in two integers: reduce1 and reduce2. Then we have merged these results using the same binary operator. This is basically how parallel streams are working.

This code is very simplified, and it is just there to show a very special property that your binary operator should have. How you split the elements of your streams should have no impact on the result of the computation. All the following splittings should give you the same result:

• 3 + (6 + 2 + 1)
• (3 + 6) + (2 + 1)
• (3 + 6 + 2) + 1

This shows that your binary operator should have a well-known property called associativity. A binary operator passed to the reduce() method should be associative.

The JavaDoc API documentation of the overloaded versions of the reduce() methods in the Stream API states that the binary operator you give as an argument has to be associative.

What is going to happen if it is not? Well, this is precisely the problem: it will not be detected, neither by the compiler nor by the Java runtime. So your data will be processed with no apparent error. You may have the right result or not; it depends on the way you data will be processed internally. In fact, if you run your code several times, you may end up with different results. This is a very important point that you need to be aware of.

How can you test that your binary operator is associative or not? In some cases it may be very easy: SUM, MIN, MAX, are well-known associative operators. In some other cases, it may be much harder. A way to check for that property can be just to run your binary operator on random data and verify if you always get the same result. If you do not, then you know your binary operator is not associative. If you do, then, unfortunately, you cannot conclude reliably.

Managing Binary Operators That Do Have Any Identity Element

The second one is a consequence of this associativity property your binary operator should have.

This associativity property is imposed by the fact that the way your data is divided should not impact the result of your computation. If you split a set A into two subsets B and C, then reducing A should give you the same result as reducing the reduction of B and the reduction of C.

You can write the previous property to the more general following expression:

A = B ⋃ C ⇒ Red(A) = Red(Red(B), Red(C))

It turns out that it leads to another consequence. Suppose things are not going well, and that B is in fact empty. In that case, C = A. The previous expression becomes the following:

Red(A) = Red(Red(∅), Red(A))

This is true if and only if the reduction of the empty set (∅) is the identity element of the reduction operation.

This is a general property in data processing: the reduction of the empty set is the identity element of the reduction operation.

This is really a problem in data processing, and especially in parallel data processing, because some very classic reduction binary operators do not have an identity element, namely MIN and MAX. The minimum element of an empty set is not defined because the MIN operation does not have an identity element.

This problem has to be addressed in the Stream API because you may have to deal with empty streams. You saw patterns to create empty streams, and it is quite easy to see that a filter() call can filter out all the data your stream is processing, thus returning a stream that will have nothing to process.

The choice that has been made in the Stream API is the following. A reduction for which the identity element is unknown (either non-existing, either non-provided) returns an instance of the Optional class. We will cover this class in more details later in this tutorial. What you need to know at this point is that this Optional class is a wrapper class that can be empty. Every time you call a terminal operation on a stream that has no known identity element, the Stream API will wrap the result in that object. If the stream you processed was empty, then this optional will also be empty, and it will be up to you and your application to decide how to handle the situation.

Exploring the Reduction Methods of the Stream API

As we mentioned earlier, the Stream API has three overloads of the reduce() methods, which we can now present in details.

Reducing with an Identity Element

The first one takes an identity element and an instance of BinaryOperator. Because the first argument you provide is known to be the identity element of the binary operator, the implementation may use that to simplify the computation. Instead of taking the first two elements of the stream to start the process, it does not take any and starts with this identity element. The algorithm used has the following form.

List<Integer> ints = List.of(3, 6, 2, 1);
BinaryOperator<Integer> sum = (a, b) -> a + b;
int identity = 0;

int result = identity;
for (int i: ints) {
    result = sum.apply(result, i);
}

System.out.println("sum = " + result);

You can notice that this way of writing things works well even if the list you need to process is empty. In that case it will return the identity element, which is what you need.

The fact that the element you provide is indeed the identity element of the binary operator is not checked by the API. Providing an element that is not will return a corrupted result.

You can see that on the following example.

Stream<Integer> ints = Stream.of(0, 0, 0, 0);

int sum = ints.reduce(10, (a, b) -> a + b);
System.out.println("sum = " + sum);

You would expect this code to print the value 0 on the console. Because the first argument of the reduce() method call is not the identity element of the binary operator, the result is in fact wrong. Running this code will print the following on your console.

sum = 10

Here is the correct code you should be using.

Stream<Integer> ints = Stream.of(0, 0, 0, 0);

int sum = ints.reduce(0, (a, b) -> a + b);
System.out.println("sum = " + sum);

This example shows you that passing a wrong identity element does not trigger any error or exception when compiling your code or running it. It is really up to you to make sure that the object you pass is indeed the identity element of your binary operator.

Testing for this property can be done in the same way as testing for the associative property. Combine your candidate identity element with as many values as possible. If you find one that is changed by the combination, then your candidate is not the right one. Unfortunately, if you cannot find any faulty combination does not necessarily mean that your candidate is correct.

Reducing with an Identity Element

The second overload of the reduce() method only takes an instance of BinaryOperator with no identity element. As expected, it returns an Optional object, wrapping the result of the reduction. The simplest thing you can do with an optional is just to open it and see if there is anything in it.

Let us an example with a reduction that does not have an identity element.

Stream<Integer> ints = Stream.of(2, 8, 1, 5, 3);
Optional<Integer> optional = ints.reduce((i1, i2) -> i1 > i2 ? i1: i2);

if (optional.isPresent()) {
    System.out.println("result = " + optional.orElseThrow());
} else {
    System.out.println("No result could be computed");
}

Running this code gives you the following result.

result = 8

Note that this code opens the optional using the orElseThrow() method, which is now the preferred way of doing so. This pattern has been added in Java SE 10, in replacement of the more traditional get() method that was originally introduced in Java SE 8.

The problem with this get() method is that it may throw a NoSuchElementException in case the optional is empty. Naming this method orElseThrow() was preferred over get(), because it reminds you that you will get an exception if you try to open an empty optional.

Many more things can be done with optionals, which you will learn about later in this tutorial.

Fusing Mapping and Reduction in one Method

The third one is a little more complex. It combines an internal mapping and a reduction with several parameters.

Let us examine the signature of this method.

<U> U reduce(U identity,
             BiFunction<U, ? super T, U> accumulator,
             BinaryOperator<U> combiner);

This method works with a type U that is defined locally to this method and used by the binary operator. The binary operator works in the same way as in the previous overloads of the reduce() method, except that it is not applied to elements of the stream but merely to mapped versions of them.

This mapping and the reduction itself are in fact combined into one operation: the accumulator. Remember that, at the beginning of this part, you saw that the reduction was conducted incrementally and was consuming one element at a time. At each point, the first argument of the reduction operation is the partial reduction of all the elements consumed so far.

The identity element is the identity element of the combiner.

This is exactly what is happening here.

Suppose you have a stream of instances of String and you need to sum all the lengths of these strings using this pattern.

The combiner combines two integers: the partial sums of the lengths of the strings processed so far. So the identity element you need to provide is the identity element: O.

The accumulator takes an element from the stream, maps it to an integer (the length of that string), and adds it to the partial sum computed so far.

Here is how the algorithm works.

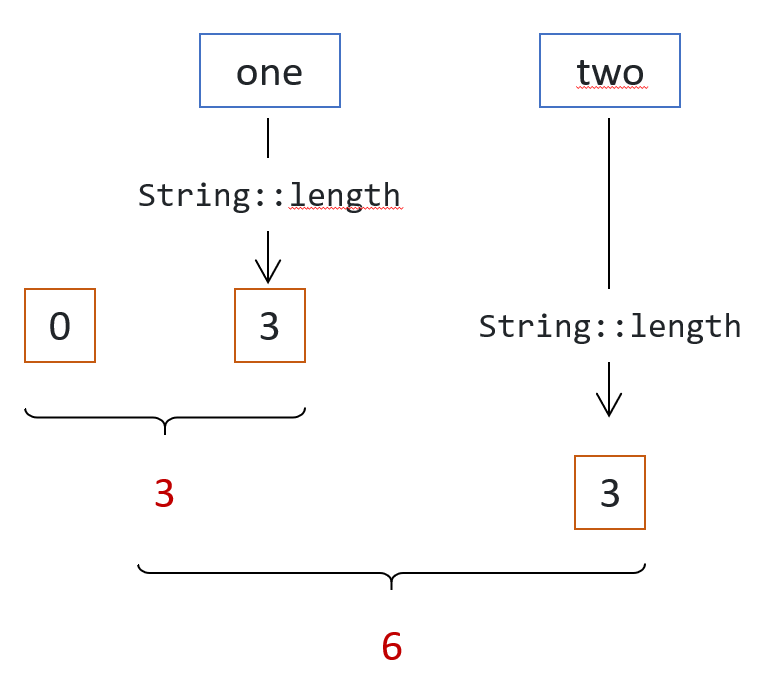
The corresponding code is the following.

Stream<String> strings = Stream.of("one", "two", "three", "four");

BinaryOperator<Integer> combiner = (length1, length2) -> length1 + length2;
BiFunction<Integer, String, Integer> accumulator =
        (partialReduction, element) -> partialReduction + element.length();

int result = strings.reduce(0, accumulator, combiner);
System.out.println("sum = " + result);

Running this code produces the following result.

sum = 15

In the example above the mapper would simply be the following function.

Function<String, Integer> mapper = String::length;

So you can rewrite the accumulator to the following pattern. This way of writing thing clearly shows the fusion of the mapping, modeled by the mapper and the reduction, modeled by the binary operator.

Function<String, Integer> mapper = String::length;
BinaryOperator<Integer> combiner = (length1, length2) -> length1 + length2;

BiFunction<Integer, String, Integer> accumulator =
        (partialReduction, element) -> partialReduction + mapper.apply(element);